Suma, resta y multiplicación
Se juega con un solo dado que se tira cuatro veces seguidas. El puntaje del primer tiro simplemente se anota. De los tres tiros siguientes, uno tiene que sumarse, uno tiene restarse y uno tiene que multiplicarse. El jugador tiene que decidirse inmediatamente después de tirar, cuál operación desea aplicar a este tiro, antes de realizar el tiro siguiente. El jugador con el mayor puntaje gana. Se pueden jugar varios turnos y sumar los puntajes.
Un ejemplo: El primer tiro fue 4, se anota. El siguiente tiro fue 2, el jugador decide restar: 4 – 2 = 2. Después tiró 5 y decidió multiplicar: 2 x 5 = 10. El último tiro fue 3, ahora necesariamente tiene que sumar porque ya usó las otras operaciones: 10 + 3 = 13. Entonces el puntaje final del jugador en este turno es 13.
Obviamente, el puntaje final depende no solamente del azar; es también necesario decidir de manera óptima acerca del orden de las operaciones. Por ejemplo, en el ejemplo anterior, el puntaje hubiera resultado mayor si el jugador hubiera primero sumado y después multiplicado: 4 + 2 = 6, 6 x 5 = 30, 30 – 3 = 27. Pero con otros puntajes, otro orden de las operaciones puede ser más ventajoso.
Acércate a 1000
Un juego con tres dados para varios jugadores. Se juega por turnos: el jugador tira los tres dados juntos, los coloca en el orden que desea (sin alterar los puntajes), y forma de los puntajes un número de tres dígitos (interpretando cada dado como un dígito). Este número se anota con el nombre del jugador; después juega el siguiente. Esto se repite hasta que cada jugador haya jugado tres turnos (o sea, tenga tres números anotados, de tres dígitos cada uno). Estos tres números se suman. Gana el jugador cuya suma es más cerca de 1000 (sin importar si la suma es por encima o por debajo de 1000).
Ejemplo: Un jugador tira primero 2, 4, 5, decide anotar 425. Después tira 1, 3, 3, decide anotar 331. Por fin tira 2, 5, 6 y anota 256. Su suma es 425 + 331 + 256 = 1012; o sea, se alejó de la meta por 12 puntos. (Si en el segundo tiro hubiera anotado 313 y en el último 265, su resultado hubiera sido mejor, porque 425 + 313 + 265 = 1003, lo que es más cerca de 1000 que 1012.)
El desafío consiste en hacer la mejor decisión en cuanto al orden de los tres dados. Por ejemplo, si los dados muestran 3, 6 y 1, se puede formar el número 136, 163, 316, 361, 613 ó 631. Es obvio que en el tercer turno, el jugador puede calcular cuál de las seis posibilidades hará que su suma final sea más cerca de 1000. Pero ¿existe también una estrategia para hacer decisiones «óptimas» en el primer y segundo turno? (Por ejemplo, si en el primer turno anoté 652, no sería aconsejable en el segundo turno colocar otra vez un 6 adelante, porque así la suma final será mucho más grande que 1000.)
24 con cuatro dados
Otro juego matemático con dados: Un jugador tira cuatro dados simultáneamente, visibles para todos. Entonces cada jugador intenta formar con los cuatro puntajes una operación matemática que dé como resultado 24. Se debe usar cada dado exactamente una vez; y se pueden usar las cuatro operaciones básicas y paréntesis. El jugador que primero encuentra una solución, recibe un punto.
Ejemplo: Los dados muestran 1, 3, 4, 4. Una solución sería (4+4) x 3 x 1 = 24.
– Obviamente, algunas combinaciones no tienen solución (por ejemplo 1, 1, 1, 1). En este caso, nadie recibe un punto. Se puede acordar un límite de tiempo, p.ej. dos minutos, y si después de este tiempo nadie tiene una solución, no hay punto y el siguiente jugador tira los dados.
Variación: Se admiten operaciones adicionales, p.ej. potencias, y formar números de varios dígitos. Así aumentan las posibilidades de encontrar una solución. Por ejemplo, con 1, 1, 2, 5 se podría formar 52 – (1 ÷ 1) = 24, ó 25 – (1 ÷ 1) = 24; y con 1, 4, 4, 6 se podría formar 144 ÷ 6 = 24. (Aunque en este caso existe también la solución «regular» 4 x (6+1) – 4 = 24.)
Yatzy
Se juega con cinco dados. Primero se prepara la lista de entradas:
|
A |
B |
C |
| 1 |
|
|
|
| 2 |
|
|
|
| 3 |
|
|
|
| 4 |
|
|
|
| 5 |
|
|
|
| 6 |
|
|
|
| Subtotal |
|
|
|
| Bono (25 p.) |
|
|
|
| Un par |
|
|
|
| Dos pares |
|
|
|
| 3 iguales |
|
|
|
| 4 iguales |
|
|
|
| «Full» o Casa llena (2 y 3) |
|
|
|
| Escalera pequeña (12345) |
|
|
|
| Escalera grande (23456) |
|
|
|
| Oportunidad |
|
|
|
| Yatzy (5 iguales) 50 p. |
|
|
|
| Total |
|
|
|
En lugar de A, B, C (etc.) se ponen los nombres de los jugadores. Por turno, cada jugador tira los dados de la siguiente manera: Primero tira los cinco dados juntos. Después puede elegir cuáles dados quiere dejar como están, y cuáles desea tirar otra vez. (Puede también elegir tirar todos los dados otra vez, o ninguno de ellos.) Del nuevo resultado, puede una vez más volver a tirar los dados que desea. Después tiene que anotar el resultado en la columna debajo de su nombre, en una fila de su elección que todavía esté libre. Las entradas tienen el siguiente significado:
1 a 6: Se anotan solamente los puntos de los dados que corresponden al número respectivo. Ejemplo: He tirado 2, 4, 4, 5, 4 y decido anotarlo en la fila «4». Entonces anoto 12 puntos, porque 4+4+4 = 12; el 2 y el 5 no puedo anotar aquí.
Subtotal (se llena al final del juego): El total de las entradas «1» a «6».
Bono (se llena al final del juego): Se pueden anotar 25 puntos si el subtotal es de 64 puntos o más. En caso contrario se anotan cero puntos en «Bono».
Un par: Dos dados deben mostrar el mismo número; se anota el total de estos dados. Ejemplo: He tirado 1, 2, 3, 3, 5, entonces se anotan 3 + 3 = 6 puntos.
Dos pares: Es necesario tener 2 pares de números iguales, p.ej. 3, 3, 5, 5, 2. Entonces anoto 3+3+5+5 = 16 puntos (el 2 no cuenta).
3 (4) iguales: Es necesario que 3 (4) dados muestren el mismo número, entonces se anota el total de estos 3 (4) dados.
Casa llena («Full»): Es necesario tener 3 números iguales, y los 2 restantes también deben ser iguales; p.ej. 2, 2, 2, 6, 6. (Se anota la suma de todos los dados.)
Escalera pequeña / grande: Los dados tienen que mostrar los números 1, 2, 3, 4, 5 (escalera pequeña) resp. 2, 3, 4, 5, 6 (escalera grande). Se anotan todos los puntos (da siempre 15 para la escalera pequeña y 20 para la escalera grande).
Oportunidad: Se anota la suma de todos los dados, sin restricciones adicionales. P.ej. 3, 5, 2, 6, 1, se anota 17.
Yatzy (5 iguales): Los 5 dados deben mostrar el mismo número. «Yatzy» vale siempre 50 puntos, sin importar el puntaje de los dados.
Total (se llena al final del juego): La suma de «Subtotal», «Bono», y todas las entradas debajo de «Bono».
En cada turno, el jugador tiene que llenar una entrada que todavía está libre. O sea, después de exactamente 15 turnos debe tener todas sus entradas llenas. Esto significa que hacia el fin del juego se verá obligado a llenar algunas entradas sin poder cumplir la condición necesaria; y en este caso tiene que escribir cero puntos en la fila respectiva. Por ejemplo, puede suceder que un jugador tenga solamente las filas «4 iguales», «Calle grande» y «Yatzy» libres, y no logra alcanzar ninguno de éstos. Entonces tiene que escribir cero puntos en una de estas filas.
El jugador con el mayor total de puntos gana.
En el transcurso de este juego es necesario hacer diversas decisiones estratégicas. Por ejemplo, si tiro tres veces el 5, ¿es mejor anotarlo en la fila «5» o en «3 iguales»? – Si en el primer intento tiro 1, 2, 4, 4, 6, ¿es mejor volver a tirar los dados 1, 2, 6 para intentar lograr tres o cuatro veces el 4; o es mejor volver a tirar los dados 1, 4 para intentar lograr la Calle grande? – Si he tirado unos números «inútiles» y ya he llenado «Oportunidad», ¿en cuál fila conviene escribir cero puntos? – Etc.
Algunas de estas preguntas se pueden responder con un poco de reflexión; otras requieren un análisis combinatorio bastante complicado. Una investigación matemática completa de este juego para encontrar la mejor estrategia, sería un desafío incluso para estudiantes universitarios.
Kalaha
Este es un juego tradicional africano para dos jugadores. Los niños africanos lo juegan en el suelo arcilloso con frejoles y otras semillas, o con piedritas. Se forman huecos en la tierra según el siguiente diseño:

(En vez de jugarlo en la tierra, se puede fabricar este juego de madera o de arcilla.) Los huecos pequeños se llaman «casas», los dos huecos grandes se llaman «almacenes». A un jugador pertenece la fila superior de casas y el almacén a la izquierda; al otro jugador pertenece la fila inferior de casas y el almacén a la derecha. Se comienza con un mismo número de semillas en cada casa (por ejemplo 3, 4, 5 ó 6 semillas en cada casa), y los almacenes vacíos. Una jugada consiste en sacar todas las semillas de una casa y «sembrarlas» en las casas adyacentes, una por una, hasta acabarlas. Se siembra según las siguientes reglas:
– Cada jugador siembra en dirección hacia su almacén, o sea (considerando el tablero como un círculo) en el sentido contrario a las agujas del reloj, una semilla en cada casa y también en su almacén.
– Si el jugador al sembrar alcanzó su almacén y todavía sobran semillas, entonces sigue sembrando en las casas del otro jugador (siempre en el sentido contrario a las agujas del reloj), y si al terminarla todavía sobran semillas, salta otra vez a su propia fila (pasando por alto el almacén del oponente) y sigue sembrando así, hasta acabar todas las semillas que sacó de la casa.
– Si la última semilla sembrada cae en el almacén, el jugador puede jugar otra vez. Esto se puede repetir varias veces, hasta que la última semilla sembrada ya no caiga en el almacén.
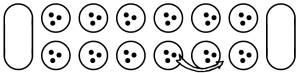
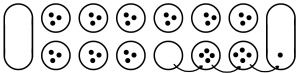
– Si la última semilla sembrada cae en una casa vacía del propio jugador, entonces puede vaciar la casa adyacente del oponente y echar todo el contenido a su almacén, junto con la última semilla sembrada.



– El juego termina cuando uno de los jugadores tiene todas sus casas vacías. Entonces, el otro jugador vacía todas sus casas a su almacén. Ganador es el que tiene más semillas en su almacén.
Master Mind (Código secreto)
Este juego para dos jugadores fue inventado recién en la segunda mitad del siglo XX (a base de un juego tradicional más antiguo), y se hizo muy popular. El tablero consiste en una caja delgada de plástico (pero se puede fabricar también de una tabla de madera) con agujeros según el siguiente diseño:

En los agujeros se colocan clavijas de diferentes colores. (Se pueden fabricar de fósforos, pintándolos con los colores necesarios). Existen clavijas de evaluación (blancas y negras), y clavijas de código (en seis colores diferentes). – El tablero tiene además cuatro agujeros escondidos en su borde trasero para el código secreto.

Una edición comercial de «Mastermind». A la derecha el código secreto que es invisible para el jugador del otro lado.
Y así se juega:
El jugador A inventa un código secreto, y el jugador B intenta adivinarlo. El jugador A establece su código, colocando cuatro clavijas de colores (sin usar las blancas ni las negras) en los agujeros escondidos, sin que el jugador B las pueda ver. Entonces B intenta adivinar el código, colocando cuatro clavijas de colores en los agujeros de la fila 1, de la forma como él piensa que podría ser el código. Obviamente, este primer intento será completamente al azar, puesto que el jugador no sabe nada acerca del código verdadero. Pero A «evalúa» cada intento de B, de manera que en el transcurso del juego se van acumulando pautas acerca del código verdadero.
Después de cada intento de B, A coloca unas clavijas blancas y/o negras en los agujeros en cuadrado de la fila correspondiente, según las siguientes reglas:
– Por cada color que se encuentra en la posición correcta (o sea, en la misma posición como en el código verdadero), se coloca una clavija negra.
– Por cada color que se encuentra en el código verdadero, pero en una posición distinta, se coloca una clavija blanca.
Entonces, B sabe el número de «aciertos» que tuvo, pero no sabe a cuáles de sus clavijas se refieren las clavijas blancas y negras. A base de esta información, hace un segundo intento en la fila 2, el cual es nuevamente evaluado por A. Y así sucesivamente, hasta que B adivina el código correcto (entonces A coloca cuatro clavijas negras como evaluación, porque todos los colores son correctos), o hasta que llegue a la fila 6 sin poder adivinar el código.
Antes de poder jugar este juego, es necesario practicar varias veces la manera de «evaluar». Si A se equivoca en una evaluación, entonces B ya no tiene la posibilidad de adivinar el código correcto, y el juego tiene que anularse. Por tanto, es importante que ambos jugadores estén bien seguros en la forma de evaluar, antes de jugar «en serio».
La siguiente ilustración muestra un juego de «Master Mind» como ejemplo. La fila superior muestra el código correcto (el cual es invisible para B.) Los comentarios abajo explican la forma como el jugador A debe evaluar las jugadas de B; y además aclaran el razonamiento de B para llegar a la solución correcta en la fila 6:

1) B colocó dos clavijas amarillas y dos celestes. Como evaluación, jugador A coloca una clavija negra por el color amarillo en la posición correcta (segunda desde la izquierda). La primera clavija amarilla colocada por B no recibe ninguna clavija de evaluación, porque este color existe una sola vez en el código original.
2) Una clavija blanca para el color amarillo en posición equivocada, y otra clavija blanca para el color rojo en posición equivocada. El color anaranjado no existe en el código original.
3) B supuso (correctamente) que la clavija negra de la fila 1 corresponde al color amarillo, y por tanto el código original debe contener amarillo en la segunda posición. (Si el color amarillo estuviera en la primera posición, hubiera recibido una clavija negra en la fila 2. Si estuviera en la tercera o cuarta posición, hubiera recibido una clavija blanca en la fila 1.) – Además, B pensó que la otra clavija blanca de la fila 2 podría referirse al color anaranjado; por tanto coloca ahora este color en posiciones distintas.
En este nuevo intento, el color amarillo es el único que figura en el código original, y está en la posición correcta: A coloca una clavija negra.
4) B sabe ahora (asumiendo que amarillo es correcto) que anaranjado y marrón no figuran en el código, y (según la fila 1) celeste tampoco. Por tanto intenta armar el código con los colores restantes. (Un desafío de razonamiento: Conociendo solamente la evaluación de los primeros tres intentos, todavía existe la posibilidad de que el código no contenga amarillo, sino que la clavija negra de la fila 1 se refiera al color celeste. ¿Cómo podría verse el código correcto en este caso?)
Evaluación: Tres clavijas negras para amarillo, rojo y verde en las posiciones correctas. Verde en la primera posición no recibe ninguna clavija de evaluación.
5) B cometió un error de razonamiento. Debería saber que la cuarta posición no puede contener rojo; de otro modo hubiera recibido una clavija negra en la fila 2. Pero concluyó correctamente que el color rojo, no el verde, debe aparecer duplicado. (El amarillo no puede estar duplicado, porque en este caso A hubiera colocado dos clavijas en la fila 1.)
Verde está en la posición equivocada (clavija blanca); amarillo está en la posición correcta (clavija negra). Rojo en la tercera posición también está correcto (otra clavija negra). Rojo en la cuarta posición recibe una clavija blanca, porque el código contiene una segunda clavija roja, pero en una posición distinta.
6) B sabe ahora que todos sus colores son correctos; solamente que la posición de dos de ellos todavía está equivocada. Con eso (y tomando en cuenta las filas anteriores) tiene suficiente información para deducir el código correcto en su último intento.
Desde un punto de vista matemático, este juego es «difícil», en el sentido de que no se puede dar ninguna estrategia generalizada que sea «óptima» en cada caso. Pero si el jugador B razona de manera consistente, y elimina todas las combinaciones imposibles, siempre será capaz de adivinar el código con 6 intentos o menos. Existe una estrategia computarizada que puede descubrir el código en un máximo de 5 intentos.
.
 Recortable para un cilindro abierto por un lado.
Recortable para un cilindro abierto por un lado. Un poco más difícil es el siguiente modelo de puente:
Un poco más difícil es el siguiente modelo de puente: Esta es una posibilidad de realizarlo como recortable. Las dos tiras delgadas arriba a la izquierda se pegan debajo de los arcos:
Esta es una posibilidad de realizarlo como recortable. Las dos tiras delgadas arriba a la izquierda se pegan debajo de los arcos: Unos modelos armados: El carro y la torre de los ejemplos anteriores, y un modelo un poco más complicado de un avión.
Unos modelos armados: El carro y la torre de los ejemplos anteriores, y un modelo un poco más complicado de un avión.























